Разрезание кубика
Для распараллеливания задач мат. физики необходимо разбить исходную сетку на набор областей и обрабатывать их все параллельно.
Описание задания
Представим, что исходная сетка представляет собой сферу. Тогда её поместить в некий ограничивающий куб, который задаётся двумя диагонально противоположными вершинами A (xmin, ymin, zmin) и B (xmax, ymax, zmax).
Программист Максим предложил следующую идею: для разбиения исходной сетки можно разбить ограничивающий куб на параллелепипеды и потом просто проверять, какие элементы сетки попали в ту или иную область.
Вот так должен выглядеть результат работы алгоритма, когда для каждого направления задан коэффициент разбиения, равный 2:
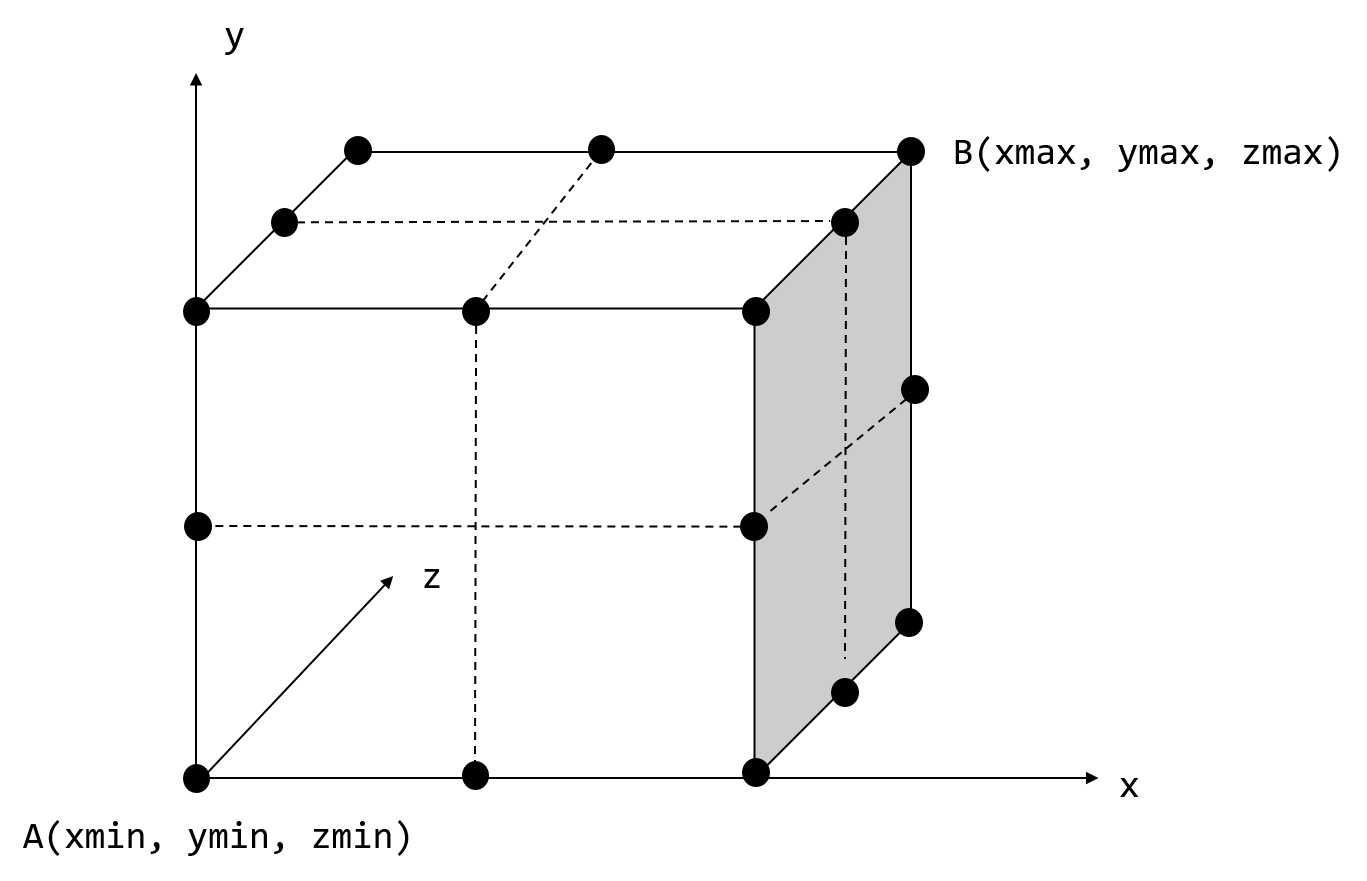
Из исходного куба получается 8 параллелепипедов поменьше, у которых также заданы координаты двух вершин.
Что нужно сделать
Реализуйте функцию Cube[] CubePartition(Cube source_cube, int x_coeff, int y_coeff, int z_coeff), которая получает на вход исходный куб и коэффициенты разбиения, а возвращает набор параллелепипедов поменьше, либо исходный куб, если все коэффициенты равны 1.
Ограничения на коэффициенты разбиения:
1 <= x_coeff, y_coeff, z_coeff <= 10
Структура для хранения куба в Си и Fortran выглядит вот так:
struct Cube {
double xmin, ymin, zmin;
double xmax, ymax, zmax;
}
type(Cube)
real(8) :: xmin, ymin, zmin
real(8) :: xmax, ymax, zmax
end type
Как видно из примеров, решение принимается либо на C/C++, либо на Fortran, если вам так проще.
Как должно работать
Здесь приведен псевдокод использования алгоритма, адаптируйте его под свой язык.
input:
xmin = 0.0, ymin = 0.0, zmin = 0.0
xmax = 1.0, ymax = 1.0, zmax = 1.0
Cube source_cube = Cube(xmin, ymin, zmin, xmax, ymax, zmax)
result_cubes[] = CubePartition(source_cube, x_coeff = 2, y_coeff = 1, z_coeff = 1)
На выходе получается два параллелепипеда.
output:
result_cubes = [
Cube(
xmin = 0.0, ymin = 0.0, zmin = 0.0,
xmax = 0.5, ymax = 1.0, zmax = 1.0
),
Cube(
xmin = 0.5, ymin = 0.0, zmin = 0.0,
xmax = 1.0, ymax = 1.0, zmax = 1.0
),
]